树

树是 n（n>=0）个节点的有限集合。

当 n=0 时，称为空树；

当 n>0 时：

1.有且仅有一个根节点

2.子节点（子集合）本身又是一颗树，称为子树

3.子树之间互不相交

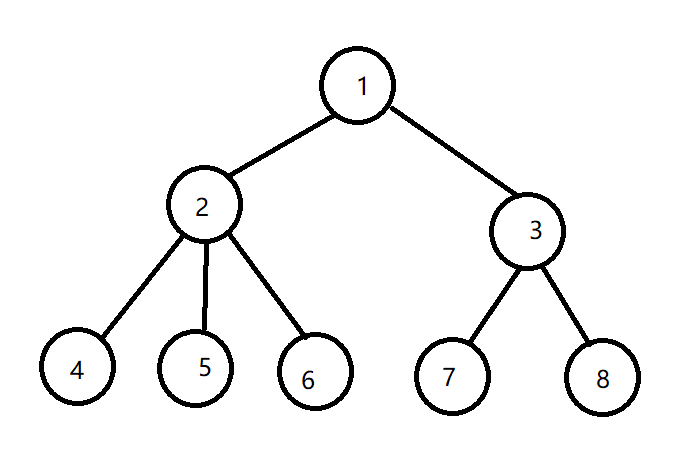
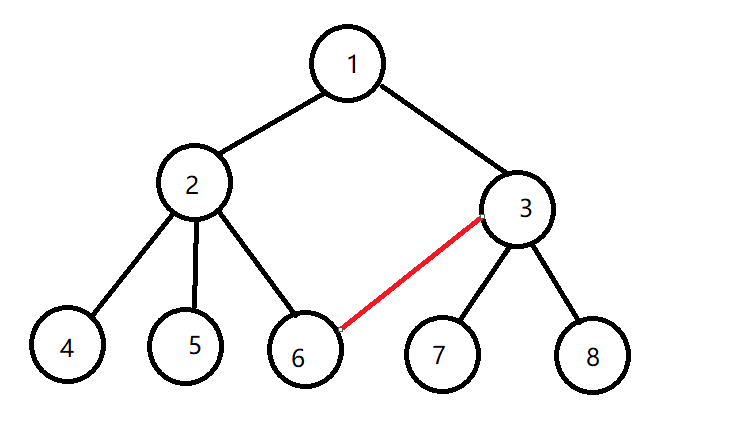
子树之间有交叉则会破坏树的定义：

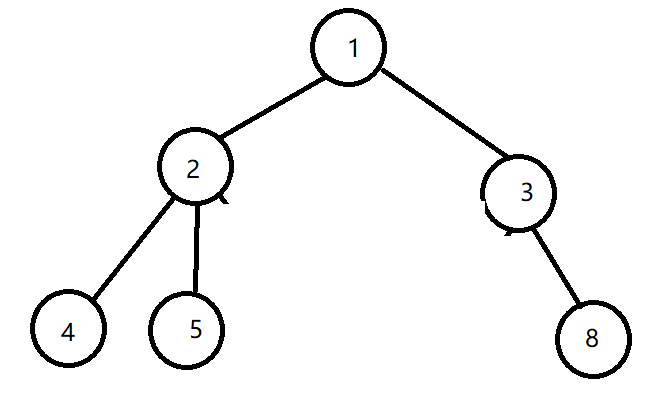
二叉树

满足 树 的特征，同时每棵树的子节点最多 2 个。

二叉排序树（二叉查找树）

满足 二叉树 的特征，同时：

1.左子树不空时，左子树所有节点的值均小于其根节点的值

2.右子树不空时，右子树所有节点的值均大于其根节点的值

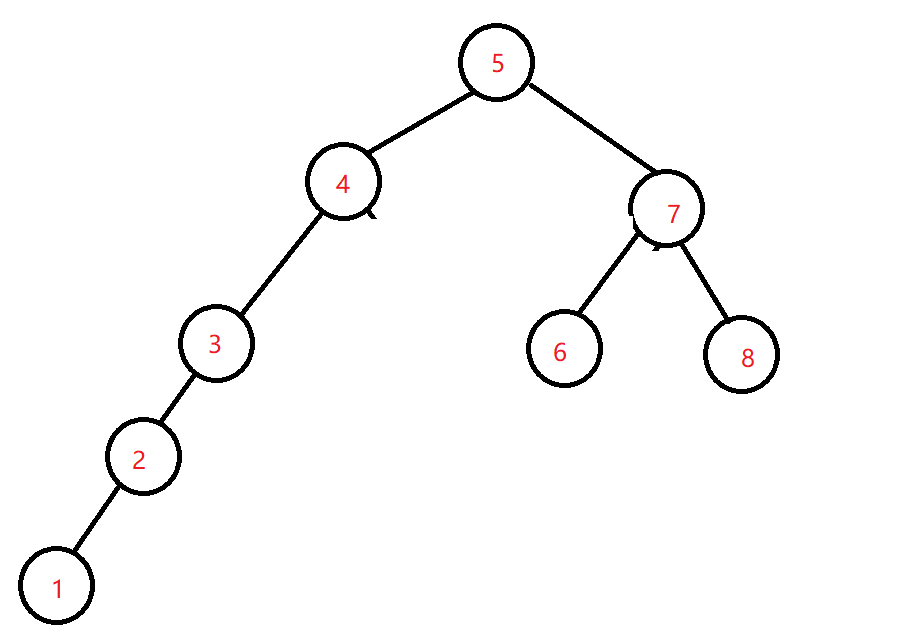
平衡二叉树

满足 二叉排序树 的特征，同时任何节点的左右高度差小于等于1。

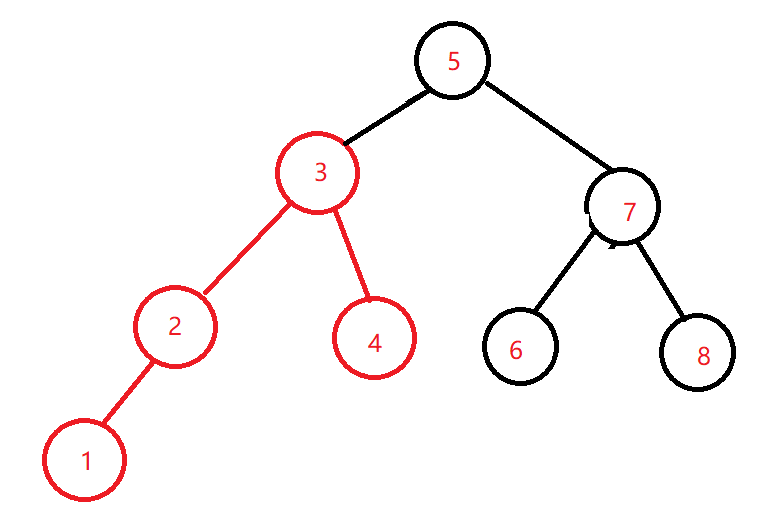
平衡二叉树，通过二叉排序树演变而来。根据二叉排序树的特征，比如当存储一系列带有顺序特性的数据时，二叉排序树容易退化成一条链，如上图以 4 为根节点的子树左右高度不平衡，因此需要通过 旋转 来满足平衡二叉树的特征，来控制树的高度。

红黑树

红黑树也是从平衡二叉树演变而来。
平衡二叉树，要求左右子树高度差不能超过1，当每次进行插入/删除操作时，几乎都需要通过旋转来保持树的平衡，频繁的旋转操作导致平衡二叉树的性能大打折扣。

红黑树通过牺牲严格的树高度平衡，来换取插入/删除操作时更少次数的旋转。

红黑树是一种自平衡的二叉查找树，但并非树高度的平衡，它的平衡是通过红黑树的特征来实现的。

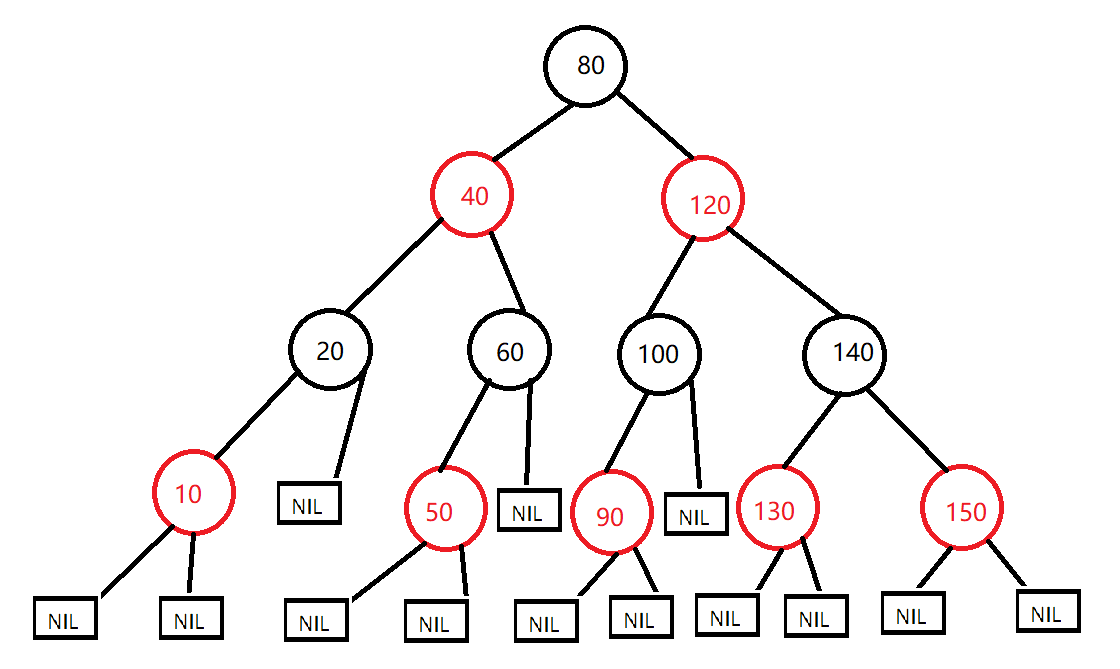
规则

1. 每个节点，不是红色，就是黑色
   
2. 根节点必须是黑色
   
3. 区别于传统的叶子节点，红黑树的叶子节点是末梢空节点（NIL），而且是黑色
   
4. 一个节点是红色，则其两个子节点必然黑色，不能出现连续的红色
   
5. 对于每个节点，从该节点开始，到其所有后代叶子节点的路径上，均包含相同数量的黑色节点